.dsy:it. (http://www.dsy.it/forum/)
- Elaborazione numerica dei segnali (http://www.dsy.it/forum/forumdisplay.php?forumid=223)
-- Dubbio trigonometrico... (http://www.dsy.it/forum/showthread.php?threadid=37395)

Dubbio trigonometrico...

Ho un dubbio sulla trigonometria base....

In pratica quando si deve calcolare la fase per lo spettro di fase si trova facendo arctan(b/a).
Molte volte capita che b non esista in quanto il coefficiente è un reale e quindi si ottiene arctan(0)... ma qua sorge il dubbio... fa 0 o pigreco?

Perchè su un compito risolto degli anni scorsi ho visto che hanno messo 0, ma in classe in un esercizio che aveva svolto l'assistente aveva messo pigreco ed in effetti sono vere entrambe perchè la tangente è 0 in 0° e 180° (pigreco)... Qualcuno sa quale bisogna scegliere? testa o croce ?

Non credo di capire bene perché dovrebbe risultare pi greco.
Ad ogni modo arctan(0) = 0 e chiunque scriva altrimenti commette un errore, anche fosse il rettore .
Inoltre, ricorda che la funzione arcotangente è limitata nell'intervallo (-PI/2, PI/2). Come potebbe valere PI, cioè 3,14?

Il grafico parla chiaro...

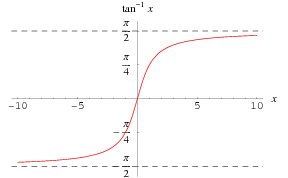
Può anche darsi che nella fretta abbia copiato male durante l'esercitazione dell'assistente... possibilissimo, ma almeno mi sono tolto un dubbio eheh.

Comunque non avevo pensato all'intervallo limitato... il mio errore è stato prendere in considerazione tutto il cerchio trigonometrico. Essendo arctan l'inverso della tangente e la tangente di pigreco è 0 ho detto "ma allora anche pigreco è arctan di 0"... peccato che non mi ricordassi che per l'appunto arctan sia definita su un intervallo invertibile -pi/2 , pi/2.... che figura eheh

Riguardando i miei appunti ho trovato la pagina compromettente e adesso ho capito perchè metteva pigreco per arctan(0).

Il ragionamento era questo:

fase = arctan(b/a) nel caso in cui uno dei due fosse stato 0 si hanno queste possibilità:

per b = 0 => se a > 0 arctan(b/a) = 0 altrimenti pigreco... infatti se si pensa alla rappresentazione trigonometrica del numero complesso, se a < 0 e b= 0, l'arco che si forma è di 180° (pigreco).

per a = 0 => se b > 0 allora pi/2 altrimenti -pi/2 per lo stesso motivo

Queste cose le ha dette l'assistente... e se non aveva bevuto prima della lezione penso che si debbano prendere per vere.

esatto vanno prese per vere, è il modo di agire negli esercizi pratici.

già che ci sono chiedo una cosa io...
nell'esempio 3.2.2 a pagina 53 della dispensa è semplice ricavare |H(vs )| = 3,16
ma perchè vs = 3,16 x 100 ? Cioè perchè per passare dalla funzione di trasferimento della ferquenza di taglio alla frequenza di taglio vera e propria moltiplico per 100? non me lo riesco a spiegare...

guarda che non moltiplica per 100 perchè deve passare a qualcos'altro... avrai perso in giro un 100 nei calcoli.

Posto la soluzione che gentilmente altri miei amici mi hanno dato così può essere utile per tutti

In pratica la frequenza di taglio è semplice perchè se |H(v)|^2 = 1/(1+(v/100)^8) significa che quella formula deve essere uguale a 1/2 che corrisponde ai famosi 3db... Quindi hai:

1/2 = 1/(1+(v/100)^8)
2= 1+(v/100)^8
1 = (v/100)^8
1 = v/100
v=100

Mentre la frequenza di stop la ottieni dai db che ti da che sono 40.
Sapendo che -20log(|H(v)|) = 40
visto che te conosci |H(v)|^2 devi fare la radice quadrata e quindi ottieni:

40 = -20log(|H(v)|)^1/2 ---- la radice la puoi mettere davanti al log per le proprietà dei logaritmi
40 = -10log(|H(v)|)
4 = -log(1/(1+(v/100)^8) ---- ora il -1 lo metti come esponente del logaritmo per le solite proprietà, ottieni quindi che si "capovolge" la frazione
4 = log(1+(v/100)^8)
10^4 = 1 + (v/100)^8
10^4 - 1 = (v/100)^8
(10^4 - 1)^1/8 = v/100
(10^4 - 1)^1/8 * 100 = v (E' qui che viene moltiplicata per 100, ma è solo frutto dei calcoli, se usi la calcolatrice esce circa 316 che è il risultato del libro)

Questo capitolo lo odio . Spero ti sia chiaro adesso. Ciao.

sì grazie millle!

Ho provato a fare questo esercizio y(n)=x(n)+2x(n-1)+x(n-2)
presente negli appunti di la.luna parte 3, lezione 23, pagina 17.
Lunedì non ero presente quindi non so se in classe è stato svolto qualcosa di simile.
Il mio problema è nel trovare H(z) in funzione di valori complessi (come negli esercizi precedenti, solo che prima erano binomi mentre questo è un trinomio), cioè alla fine riduco la funzione a qualcosa da cui possa ricavare modulo e fase in maniera intuitiva, solo che il modulo mi viene traslato: [2cos(2pigreco.omega)+2]
è possibile?
e nel disegnarlo graficamente (oltre alla traslazione) ho notato un altro problema, all'aumentare della frequenza i valori tendono prima a diminuire in potenza e poi ad aumentare (in valori negativi), in questo caso quindi non è nè un filtro passa basso nè un filtro passa alto?
In conclusione spero proprio di aver sbagliato i calcoli quindi se qualcuno ha fatto questo esercizio (o ha voglia di farlo) e sa dirmi come gli vengono modulo e fase di H(z) me lo faccia sapere :S

Per prima cosa, per consentire anche agli altri di consultare meglio il forum, ti consiglio di aprire un thread apposito se hai degli argomenti non troppo affini a questo post... se no si rischia di andare off topic.

Ad ogni modo, sì, ha svolto esercizi simili a lezione e il trucco sta nel considerare anche il 2 moltiplicato per l'esponenziale.
Fermandoti un po' prima della trasformazione in coseno avrai una serie di reali per esponenziali. Il tuo 2 non l'hai raccolto perchè non ti è venuto in mente di fare (la O sta per omega):

2 * e^(iPIO) * e^(-iPIO)

In questo modo gli esponenti si sommano e viene 0, e^0 = 1, 2*1 = 2... quindi puoi farlo, dopodichè raccogli l'esponenziale.
Anche gli altri esponenziali se ti trovi con i 2PI al posto del PI, per raccogliere gli scorpori sempre come moltiplicazioni tra esponenziali usando le solite regole per la somma di potenze.... sempre che serva, ovviamente usi l'esponenziale a te più comodo per raccogliere a fattor comune.

I soliti trucchetti matematici... Ciao.

Riguardando i miei appunti ho trovato la pagina compromettente e adesso ho capito perchè metteva pigreco per arctan(0).

Il ragionamento era questo:

fase = arctan(b/a) nel caso in cui uno dei due fosse stato 0 si hanno queste possibilità:

per b = 0 => se a > 0 arctan(b/a) = 0 altrimenti pigreco... infatti se si pensa alla rappresentazione trigonometrica del numero complesso, se a < 0 e b= 0, l'arco che si forma è di 180° (pigreco).

per a = 0 => se b > 0 allora pi/2 altrimenti -pi/2 per lo stesso motivo

Queste cose le ha dette l'assistente... e se non aveva bevuto prima della lezione penso che si debbano prendere per vere.